Domain Relational Calculus

• Domain Relational Calculus uses domain variables that take on values from an attributes domain, rather than for an entire tuple. ​
• Formal Definition​
• An expression in the domain relational calculus is of the form :​
• {<x1, x2, …..., xn> | P(x1, x2, …..., xn)}​
• Where ​
• x1, x2, …..., xn represent domain variables.​
• P formula composed of atoms. ​
• An atom in the domain relational calculus has one of the following forms:​
• <x1, x2, …..., xn> ϵ r, where r is a relation on n attributes and x1, x2, …..., xn are domain variables or domain constants.​
• X Θ y, where x and y are domain variables and Θ is a comparison operator (<, ≤, >, ≥, = , ≠) Attributes x and y have domains that can be compared by  Θ ​
• x Θ c, where x is a domain variable, Θ  is a comparison operator, and c is a constant in the domain of the attribute for which x and a domain variables. ​

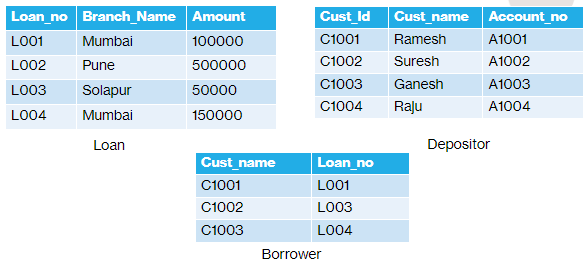
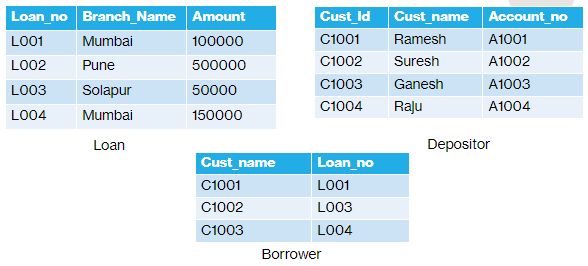
Examples based on following relation.

Example1: Find the loan number, branch name and amount for loans of over 100000

Answer: =>      { < l, b, a > | < l, b, a > ϵ loan ᴧ a > 100000 }​

Example2: Find the name of all customer who have a loan from the Mumbai branch

Answer: =>  { < c, a > ∃ l ((<c, l > ϵ borrower ᴧ ∃ b(<l, b, a >  ϵ loan ᴧ b = "Mumbai") }​

 

Tuple Relational Calculus

• The tuple relational algebra is a nonprocedural query language. It describes the desired information without giving a specific procedure or obtaining that information.​
• A query in the tuple relational calculus is expressed as ​
• { t | P(t) }​
• That is, it is the set of all tuples t such that predicate P is true for t.​
• In tuple relational calculus ​
• t[A] - denotes the value of tuple on attribute A.​
• t ε  r –denotes tuple t in relation r. ​

Examples based on the following table

Example 1: Find all tuples from the depositor relation

Answer: { t | t ϵ depositor }​

Example 2: Find the loan_no, branch_name and amount for loans of over 100000.

Answer: { t | t ϵ loan ᴧ [amount] > 100000 }​

Distributed Transaction

A distributed transaction is a set of operations on data that is performed across two or more data repositories (especially databases). It is typically coordinated across separate nodes connected by a network, but may also span multiple databases on a single server.

Distributed Transaction Demo Code (Java + MySQL)

// Demo Implementation of Distributed Transaction
importjava.sql.*;
importjava.sql.DriverManager;
importjava.sql.PreparedStatement;
importjava.sql.ResultSet;
importjava.sql.Savepoint;
importjava.sql.Statement;
importjava.util.Scanner;
importjava.sql.Connection;

publicclass Distributed {
/**
*@paramargs
*/
publicstaticvoid main(String[] args) {
// TODO Auto-generated method stub
Scanner sc=newScanner(System.in);
System.out.println("Enter Your Account Number:");
intfromAccountNo=sc.nextInt();
System.out.println("Enter Reciever Account Number:");
inttoAccountNo=sc.nextInt();
System.out.println("Enter Amount to be Transferred:");
int amount=sc.nextInt();
String url = "jdbc:mysql://localhost:3306/transaction";
String url1 = "jdbc:mysql://localhost:3306/tran";
String driver = "com.mysql.jdbc.Driver";
String user = "root";
String pass = "root";
PreparedStatementpst=null;
ResultSet res=null;
ResultSet r1=null;
Connection con=null;
Statement st=null;
Statement st1=null;
intfromBalance=0;
inttoBalance=0;

try{
Class.forName(driver);
con=DriverManager.getConnection(url, user, pass);
con.setAutoCommit(false);
Connection con1 = DriverManager.getConnection(url1, user, pass);
Savepoint save1=con.setSavepoint();
st =con.createStatement(ResultSet.TYPE_SCROLL_SENSITIVE,ResultSet.TYPE_FORWARD_ONLY);
String str="SELECT BALANCE from SBH where ACCOUNT_NUMBER="+fromAccountNo+"";
res = st.executeQuery(str);
while(res.next()){
System.out.println(str);
fromBalance= res.getInt(1);
System.out.println(+fromBalance);
}
fromBalance=fromBalance-amount;
pst=con.prepareStatement("UPDATE SBH SET BALANCE=? WHERE ACCOUNT_NUMBER=?");
res.first();
pst.setInt(1, fromBalance);
pst.setInt(2, fromAccountNo);
int re= pst.executeUpdate();
System.out.println("hii");
if(re!=0){
st1= con1.createStatement();
String strnew="SELECT BALANCE from BOI where ACCOUNT_NUMBER="+toAccountNo+"";
System.out.println(+toAccountNo);
st1 = con1.createStatement(ResultSet.TYPE_SCROLL_SENSITIVE,ResultSet.TYPE_FORWARD_ONLY);
//System.out.println("hiivvhh11");
r1= st1.executeQuery(strnew);
//System.out.println("hiivvhh");
while (r1.next())
{
toBalance = r1.getInt(1);
System.out.println("hiiii second");
}
toBalance=amount+toBalance;
PreparedStatement pst1 = con1.prepareStatement("UPDATE BOI SET BALANCE=? WHERE ACCOUNT_NUMBER=?");
pst1.setInt(1, toBalance);
pst1.setInt(2, toAccountNo);
int re1= pst1.executeUpdate();
if(re1!=0){
System.out.println("Amount Transferred Successfully");
con.commit();
}else{
System.out.println("Unable to transfer");
con.rollback(save1);
}
}
}
catch(Exception e){
}
}
}

Modification of the Database in Relational Algebra

• Different operations that modify the contents of the database are​
• Delete​
• Insert​
• Update​
• We express database modification by using the assignment operation.​

Deletion

• The deletion operation removes the selected tuples from the database using delete values of any particular attribute.​
• In relational algebra a deletion is expressed by​
•  r ← r - E​
•  r is a relation​
• E is a relational algebra query​

Example​

Delete 'Ramesh' Record from the database​

• employees ← employees - σemp_name='Ramesh'(employees)

• Delete all employee working in IT department​
• employees ← employees - σdepartment='IT'(employees)

Insertion

• The relational algebra expresses an insertion by ​
• r ← r Ս E​
• r is a relation​
• E is relational algebra expression​

Examples​

• Insert Ramesh Record in employee relation​
• employees ← employees Ս {('E004','Ramesh', 12000)}​

Updating

• Sometimes, we wish to change a value in a tuple without changing all values in the tuple. We can use generalized projection operation to do this:​

• r  ← ∏f1,f2,f3...fn(r)

• Where fi the ith attribute to be updated has expression involving constants and attributes of r, that gives new value for the attribute. ​

• Example​
• ∏emp_id, salary*1.05(employees)

Union, Intersection and Difference Cartesian Product and Additional Operations (Natural Join, Division, Assignment, Generalized Projection, Aggregate Functions, Outer Join ) ​ in Relational Algebra

• The Union, Intersection and Difference operations requires following condition ​
• The two relation/table must contain the same number of columns ​
• Each column of the first relation/table must be either the same data type as the corresponding column of the second relation/table or convertible to the same data type as corresponding column of the second. ​

Union

The result of operation is denoted by depositor Ս borrower, is the relation that includes all tuples that are either in depositor or borrower or both. Duplicates are eliminated. ​

Intersection

The Result of intersection operation is a relation that includes all tuples that are in both depositor and borrower. It is denoted by depositor ∩ borrower.​

Difference

The difference operation is denoted by depositor – borrower. ​

The result of the difference operator is the relation that contain all tuples in depositor but not in borrower. 

• Both Union and intersection operations are commutative and associative ​
• AUB =BUA  and  A∩B=B∩A​
• AU(BUC)=(AUB)UC  and A∩(B∩C)=(A∩B)∩C​

• The difference operation is not commutative.​
• A-B≠B-A​

Cartesian Product

• It is known as CROSS PRODUCT or CROSS JOINS.​
• It is denoted by 'x'​
• The Cartesian product of two relations A and B is denoted by AxB​
• The result of cartesian product of two relation which have X and Y columns is relation that has X+Y Columns. The resulting relation will have one tuple or each combination of tuples from each participating relation. ​
• If a relation have m and n tuples, then the CARTESIAN PRODUCT will have m x n tuples.​

Additional Operations

We define additional operations that do not add any power to the relational algebra, but that simplify common queries.​

• Set intersection​
• Natural join​
• Assignment​
• Outer join ​

Natural Join

The natural join is a binary operation.​

It is denoted by the join symbol ⨝​

The natural join operation forms a cartesian product of its two arguments, performs a selection forcing equality on those attributes that appear in both relation schemes and finally removes duplicate attributes.​

The difference between natural join and cartesian product is : the query involving cartesian product includes a selection operation on the result of the cartesian product. ​

Consider following schema​

• employee(emp_id, emp_name)​
• salary(emp_id,salary)​

• Πemp_name,salary(σemployee.emp_id=salary.emp_id(employee x salary)) = Πemp_name,salary(employee  ⨝ salary)

• The query using natural-join is simpler than cartesian product query. ​

Πemp_name,salary(employee  ⨝ salary)​

Division Operator​

• The division operation is denoted by '÷' it is used for the queries include the phrase 'for all' / 'for every'.​
• A(X,Y)÷B(Y) will results X values for that there should be tuple <x,y> for every Y value of relation B.

Division Example

List the E_id  of works relation worked for all /every projects  of Projects relation 

The Assignment Operator

• The assignment operation is denoted by '←'. ​
• It works like assignment in programming language​
• Example t1←σroll_no=1(students)
• The result of right side expression is assigned to the relation variable on the left. ​
• With assignment operation, a query can be written as a sequential program consisting of a series of assignment followed by an expression whose value is displayed as the result of the query. ​
  

Extended Relational Algebra Operations

• The basic relational-algebra operations have been extended in several ways​
• A simple extension allow arithmetic operations as part of project.​
• An important extension is, allow aggregate operations such as computing the sum of set, or their average.​
• Another important extension is outer join operation, which allow relational algebra expression to deal with null values. ​

Generalized Projection

• The generalized projection operation extends the projection operation by allowing arithmetic function to be used in the projection list. ​
• It is in the form of ∏f1,f2,f3,…,fn(E) where E: relation algebra expression and f1,f2,f3... are an arithmetic expression involving constants and attributes of E. ​
• Example  :  ∏emp_id, salary*1.05(employees)

Aggregate Functions

• Aggregate Functions take a collection of values and return a single value as a result. ​
• It is represented 'calligraphic G'  '𝒢'​
• 𝒢sum(salary)(employees)

• Display the sum of salary of employees​

• 𝒢count(emp_id)(employees)

• Count the number of employees in employees relation​
• The 𝒢 signifies that aggregate function is to be applied and subscript specifies the aggregate operation to be applied.​

Outer Join

It is extension of the join operation to deal with missing information. ​

In the below example the record of Raju was missing in the outcome of natural join ​

• To avoid the loss of information, we can use outer join operation.​
• There are three forms of outer-join​

1. Left Outer-join​
2. Right Outer-join​
3. Full Outer-join​

Left Outer-join

• It is denoted by ⟕​
• It take all tuples in the left relation and matching records of right relation, pads the tuples with null values for all other attributes from the right relation. ​

Right Outer-join

• It is denoted by ⟖​
• It take all tuples in the right relation and matching records of left relation, pads the tuples with null values for all other attributes from the left relation. ​

Full Outer-join

• It is denoted by ⟗​
• It take all tuples in the right relation and all the tuples from left relation, pads the tuples with null values for non-matching attributes from the left and right relation. ​

Joins Summary 

The Select, Project & Rename Operation​ in Relational Algebra

The Select Operation​

• The select operation select tuples that satisfy a given predicate.​
• The small Greek letter sigma(σ) is use to denote select operation​
• The predicate appears as a subscript to σ​
• The Comparison operator =,≠,<,>,≤,≥​
• The Connectives and(∧ ), or( v), not(¬)​

  

Examples

• To Select the tuples from employee relations those employees belong to CSE Department
• σdept_name='CSE'(employees)​

• The employees whose salary greater than 12000/-​
•  σemp_salary>12000(employees)

• Department is CSE and Salary is greater than 12000/- ​
• σdept_name='CSE' ∧ emp_salary>12000(employees)​

Project Operation

• It is Unary operation​
• It selects certain columns from a table while discarding others. ​
• It removes any duplicated rows from the result relation.​
• Denoted by the uppercase Greek letter pi (Π)​
• The attribute list appears in the subscript to  Π  with argument relation in parentheses. ​

Examples:

• ΠId,name,dept,salary(employees)
• Selects only id, name, dept_salary Form employees relation.​

• Πtitle,Author(Book)
• Display all title and author from book relation

Composition of Relation Operations

• The relational-algebra operations can be composed together into a relational-algebra expression it is just like composing arithmetic operations into athematic expression. ​

• Example​
• Πname(σdept_name='CSE'(employees))

Rename Operation

• In Relational algebra, we can rename either the relation or the attributes or both.​
• It is denoted by lowercase Greek letter rho (ρ)​
• ρs(new attribute name)(R)
• ρs(R)
• ρ(new attribute name)(R)

Examples:

• ρt1(fn,ln,sal)(R)

• Rename relation R with new relation t1 with  new name for the listed attributes ​

• ρ(fn,ln,sal)(R)

• Rename only attributes listed in the brackets.​

• ρt1(R)

• Rename only relation R with new name t1.​